2.2.1. Расчет основных параметров рабочих органов и режима работы почвообрабатывающих машин и орудий /3.1.16/.

• Задачи.
• Решения.

Рисунок 1.1. Задача 2.2.1.1. Определить, при какой глубине aпр вспашки корпусом без предплужника пласт почвы окажется в предельно-устойчивом положении, если ширина захвата корпуса b = 35 см. (см. Рис. 1.1.) Ответ: aпр = 27,56 см Решение.

Рисунок 1.2. Задача 2.2.1.2. Ширина захвата корпуса b = 35 см., глубина вспашки a = 22 см. Рабочая поверхность корпуса культурного типа. Угол минимального наклона горизонтальной образующей к стенке борозды min = 39,5o, угол максимального наклона max = 45o. Определить угол наклона горизонтальной образующей на высоте Z = 22,5 см от дна борозды. Принять Z1 = 7,5 см. Указания. На рис. 1.2. представлена закономерность изменения угла 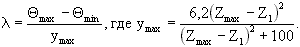в зависимости от Z - высоты расположения горизонтальной образующей над дном борозды. Из графика следует, что любое промежуточное значение угла равно = min + . В интервале высот от Z1 до Zmax приращение угла = y, где - масштабный коэффициент; Масштабный коэффициент: Ответ: = 43,64o Решение.

Рисунок 1.3. Задача 2.2.1.3. Максимальная высота корпуса плуга с полувинтовой рабочей поверхностью Zmax = 42 см. Угол наклона лезвия лемеха к стенке борозды 0 = 38o, угол минимального наклона горизонтальной образующей к стенке борозды min = 35o, угол максимального наклона max = 45o. Определить углы ' и " наклона горизонтальных образующих поверхности корпуса, расположенных на высоте 27,5 см от дна борозды. Принять высоту расположения образующей с минимальным углом наклона Z1 = 7,5 см. Указания. Вид закономерности изменения угла в зависимости от высоты Z представлен на рис. 1.3. Любое промежуточное значение угла наклона образующей равно = min + , где = y = x2 / 2p. Масштабный коэффициент принимаем = 1 град/см. В интервале значений Z от 0 до Z1, y = X2 / 2 p, где X = Z - Z1 и 2p1 = (0 - Z1)2 / (0 - min). Для Z от Z1 до Zmax, y = X2 / 2p2, где X = Z - Z1 и 2p2 = (Zmax - Z1)2/ (max - min).

Ответ: 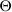' = 35,33^o; 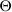" = 38,36^o. Решение.

Задача 2.2.1.4. Определить усилие P_ш в штоке гидроцилиндра при подъеме прицепного плуга в транспортное положение.
Исходные данные: схема подьемного механизма, размеры и расположение звеньев (рис. 1.4.), реакции колес с учетом веса почвы: R_n' = 5816 H, R_б' = 9032 Н, усилие в горизонтальной тяге P₃ = 0.

Ответ: P_ш = 35934 Н. Решение.

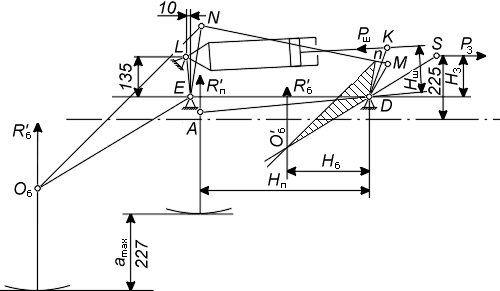Рисунок 1.4.

Рисунок 1.5. Задача 2.2.1.5. Определить усилие P в штоке гидроцилиндра, необходимое для уравновешивания навесного плуга весом G = 6000 Н в транспортном положении. Схема подъемного механизма задана (рис. 1.5.). Ответ: P = 9538 H. Решение.

Задача 2.2.1.6. Определить длину L_p полевой доски корпуса плуга при ширине захвата 75 см, угле наклона лемеха к стенке борозды 40^o и коэффициенте трения почвы о поверхность лемеха 0,6.

Ответ: L_p = 153 см. Решение.

Задача 2.2.1.7. Динамометрированием установлено, что тяговое усилие прицепного пятикорпусного плуга при вспашке на глубину a_H = 20 см и наскорости V = 1,2 м/c равно P_H = 16560 H; вес плуга G_H = 12600 H; ширина захвата корпуса b = 35 см. Определить расчетное тяговое усилие P плуга при вспашке в тех же условиях, но при глубине a = 25 см и числе корпусов n = 4 (вес одного корпуса 1000 H). Расчет выполнить по формуле акад. Горячкина (коэффициенты: f=0,4; K=28x10³ Па; = 2000 Hc²/м⁴) и по упрощенной формуле; найти разницу в расчетах.

Ответ: P = 15448 H. P' = 16555 H. (По упрощенной формуле). Решение.

Задача 2.2.1.8. Построить зубовое поле, определить форму рамы и ширину захвата b_p средней зубовой бороны при следующих условиях: число поперечных рядов зубьев M = 5, число зубьев в ряду N = 4, расстояние между поперечными рядами зубьев L = 300 мм, между соседними следами зубьев a = 50 мм, число ходов основного винта К₁ = 3.

Решение.

Задача 2.2.1.9. Определить расчетом расстояние b между смежными дисками лущильника при установке дисков под углом 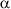= 35^o к линии тяги и из условия получения гребней высотой не более С = 30 мм. Диаметр диска D = 450 мм. Вычертить расчетную схему в масштабе.

Решение.

Задача 2.2.1.10. Определить диаметр D и угол наклона 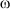образующей конуса заточки к плоскости режущей кромки и радиус R кривизны рабочей поверхности сферического диска лущильника при следующих условиях: глубина обработки почвы a = 8 см, угол атаки 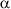= 35^o, затылочный угол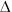 _a = 5^o, угол заострения режущей кромки i = 15^o.

Ответ: D = 510 мм; 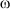= 38,42^o; R = 660 мм. Решение.

Задача 2.2.1.11. Сферический диск характеризуется следующими параметрами: диаметр D = 450 мм, радиус кривизны рабочей поверхности R = 600 мм, угол заострения режущей кромки i = 25^o, угол атаки 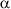= 35^o. Определить затылочный угол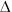 _a на глубине хода a = 8 см.

Ответ: 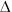_a = -4,34^o. Решение.

Задача 2.2.1.12. Определить угол 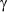раствора лезвий стрельчатой полольной лапы, если коэффициент трения стеблей сорных растений о лезвие f = 0,97. Дать расчетную схему.

Ответ: Угол раствора лезвий стрельчатой лапы 2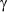 <= 91,8^o. Решение.

Задача 2.2.1.13. Рыхлительная лапа шириной b = 4 см наклонена к горизонту под углом 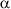= 28^o и установлена на глубину обработки почвы a = 12 см. Определить ширину b полоски, обрабатываемой лапой, а также расстояние B между соседними лапами в ряду и расстояние L между рядами лап. Начертить схему размещения лап в принятом масштабе. Коэффициент трения почвы о поверхность лапы f = 0,47, угол между сечениями, ограничивающими деформацию почвы с боковых сторон 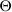= 50^o, вылет лапы l₀ = 20 cм, перекрытие полосок рыхления 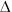b = 3 см.

Ответ: b = 22,67 cм, B = 59 см, L = 36 см Решение.

Задача 2.2.1.14. Определить подачу X_z на нож пропашной фрезы, построить траекторию абсолютного движения двух последовательно работающих друг за другом ножей и определить расчетную толщину 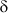стружки, снимаемой ножом, при следующих условиях: диаметр барабана D = 350 мм, частота вращения его n = 240 мин^-1, число ножей на секции Z = 6 (три ножа с левым загибом и три ножа с правым загибом), глубина обработки почвы a = 10 см, скорость перемещения машины v_м = 1,1 м/с.

Ответ: X_z = 92 мм, 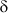= 83,06 мм. Решение.

Рисунок 1.6. Задача 2.2.1.15. Определить частоту вращения n фрезерного барабана диаметром D = 350 мм при скорости перемещения машины vм = 1,4 м/c и глубине обработки почвы a = 10 см. В момент входа ножа в почву абсолютная скорость его направлена вертикально вниз.(Рис. 1.6.) Ответ: n = 178 мин-1. Решение.

Задача 2.2.1.16. Определить показатель 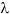кинематического режима работы фрезы из условия получения гребешков на дне борозды высотой h_г = 2 см. Диаметр фрезерного барабана D = 350 мм, число ножей Z = 4, коэффициент, учитывающий скалывание почвенной стружки K = 0,5.

Ответ: 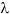= 2,3. Решение.

Задача 2.2.1.17. Определить мощность N, необходимую для работы прицепной болотной фрезы на фрезеровании луговой дернины при следующих условиях: ширина захвата B = 2 м, диаметр фрезерного барабана D = 710 мм, частота вращения его n = 234 мин^-1, общее число ножей Z = 120, на одной секции закреплено 4 ножа с загибом влево и 4 ножа с загибом в право; один нож снимает стружку почвы шириной b_c = 6,7 см, глубина обработки почвы а = 20 см, скорость перемещения фрезы v_м = 0,875 м/с. Вес фрезы G = 20000 H, коэффициент сопротивления деформации почвы К_д = 0,15 МПа, плотность почвы r = 1300 кг/м³.

Ответ: Полная мощность N = 64,68 кВт. Решение.

Решения задач.

Рисунок 1.1. Задача 2.2.1.1. На рис.1.1 показана схема отваленных пластов в предельно-устойчивом положении. Из подобия треугольников Д'В'С' и Д'В"Д" имеем . Обозначив K = b / a, после преобразований получим: K4 - K2 - 1 = 0. Решая уравнение, находим Kпр = 1,27; это предельное значение отношения b / aпр; тогда предельное значение глубины вспашки будет равно: aпр = b / Kпр = 35 / 1,27 = 27,56 см.

Задача 2.2.1.2.(см.Рис.1.2.) Максимальная высота корпуса ; для a = 22 см, H2 = 0; ; ; = (45o - 39,5o)/ 5,7 = 0,965 град/см; = y = 0,965 x 4,29 = 4,14o; = min + = 39,5o + 4,14o = 43,64o.

Рисунок 1.2.

Задача 2.2.1.3.(см.Рис.1.3.) 1) Определяем угол наклона горизонтальной образующей при Z = 5 см: ' = min + (X2 / 2p1); min = 35o; X = 5 - 7,5 = -2,5 см; 2p1 = (0 - 7,5)2 / (38o - 35o) = 18,75 см; '= 35o+ (-2,5)2 / 18,75 = 35,33o. 2) Находим значение угла " для Z = 27,5 см; "= min + (X2 / 2p2); X= 27,5 - 7,5 = 20 см; 2p2 = (42 - 7,5)2 / (45o - 35o) = 119 см; " = 35o+ 202 / 119 = 38,36o

Рисунок 1.3.

Задача 2.2.1.4.
1. Вычерчиваем в масштабе схему механизма и прикладываем к нему внешние силы: R'_п, R'_б и Р_ш.
2. Определяем графо-аналитическим методом скорости v_а, v_об и v_к точек приложения внешних сил с помощью плана скоростей.
Построение плана скоростей с полюсом в точке D показано на рис.4. Скорости точек приложения сил равны: v_а = DА, v_об = DО'_б, v_к = DК.
3. Находим плечи действия сил и составляем уравнение моментов сил относительно полюса D:
R'_пH_п + R'_бН_б - Р_шН_ш = 0
4. Находим усилие на штоке гидроцилиндра: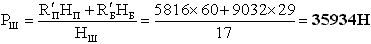

Рисунок 1.4.

Рисунок 1.5. Задача 2.2.1.5. Строим план скоростей, повернутый на 90o с полюсом в точке D. Скорость точки F: VF = D f, скорость точки K: Vk = D K'. Плечи действия сил равны отрезкам HG и HP. Составляем уравнения моментов сил G и P. Усилие на штоке гидроцилиндра: P = G HG / HP = 6000 x 64 / 13 = 29538 H.

Рисунок 2.1. Задача 2.2.1.6. При движении корпуса в почве на него действуют силы сопротивления, которые стремятся повернуть корпус относительно оси, проходящей через центр тяжести. Устойчивость корпусу в борозде придает полевая доска. Для выполнения своего назначения полевая доска должна иметь определенную длину LP. При определении длины полевой доски исходят из предположения акад. В.П. Горячкина, что основное сопротивление сосредоточено на середине лемеха. На основании этого считают достаточным соблюдать условие, при котором проекция силы сопротивления R, действующей на середину лемеха, при своем продолжении встречает пятку полевой доски. Линия действия силы R (рис. 2.1.) отклоняется от нормали к лезвию лемеха на угол трения = arctg f = arctg 0,6 = 31o. Из расчетной схемы можно записать

Задача 2.2.1.7. Формула акад. Горячкина: P = fG + kab + aBV².
Вес плуга G = 12600 - 1000 = 11600 H,
Ширина захвата плуга B = bn = 35 x 4 = 140 см = 1,4 м.
Сила тяги P=0,4 x 11600 + 28000 x 0,25 x 1,4 + 2000 x 0,25 x 1,4 x 1,22 = 4640 + 9800 + 1008 = 15448 H.
Упрощенная формула: P^* = K^*ab, где К^* - коэффициент удельного сопротивления почвы, определяем его из начальных условий: Р_н = 16560 Н, а_н = 20 см, В_н = 175 см, К^* = Р_н / (а_н x В_н) = 16560 / (20 x 175) = 4,73 Н/см²
Сила тяги Р^* = К^*аВ = 4,73 x 25 x 140 = 16555 Н.
Разница в расчетах 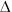Р = 16555 - 15448 = 1107 Н.

Рисунок 2.2. Задача 2.2.1.8. Указания. Зубовое поле строят по развертке двух винтов на плоскость. Сумма заходов основного и дополнительного (обратного) винтов должна быть равна числу поперечных рядов зубьев, то есть К1 + К2 = 5. Если К1 = 3, то К2 = 2. Шаг основного винта t1 = К1 b, дополнительного t2 = К2 b (рис. 2.2.). Линия АВ - развернутая винтовая линия основного винта, линия ВС - развернутая винтовая линия дополнительного винта. Расстояние между соседними развернутыми винтовыми линиями или расстояние между зубьями в ряду b = М x а. С целью обеспечения "спокойного" хода бороны боковые контуры рамы делают зигзагообразными ( контуры cdef и c'd'e'f'). Во избежание огрехов отрезки cd и ef направляют по развертке трехходового (основного) винта, а отрезки de и d'e' - по развертке двухходового (дополнительного) винта. Планки рамы у средних и тяжелых борон имеют прямолинейную форму. Их направляют по развернутым винтовым линиям основного и дополнительного винтов. Зубья (по четыре зуба в ряду) размещают в точках пересечения планок. Ширина захвата бороны Bр = М x N x a = 5 x 4 x 50 = 1000 мм.

Задача 2.2.1.9. Из рис. 2.3. следует, что расстояние между смежными дисками при высоте гребней С и угле атаки равно b = Dс tg , где

Рисунок 2.3.

Рисунок 2.4. Задача 2.2.1.10. 1) Диаметр диска определяют в зависимости от заданной глубины обработки из соотношения К = D/а, где К = 6...8. Примем К = 6, тогда D = 6 x 80 = 480 мм. Принимаем диаметр диска D = 510 мм ( ГОСТ 198...75). 2) Угол наклона образующей конуса заточки к плоскости режущей кромки (рис. 2.4) где Dа - хорда погружения диска на глубину а; угол а = - а = 35o - 5o = 30o. Угол = arctg ( 510/371 x 0,577 ) = 38,42o. 3) Угол, характеризующий кривизну рабочей поверхности диска = - i = 38,42o - 15o = 23,42o 4) Радиус кривизны рабочей поверхности диска R = D/ (2 x sin) = 510/( 2 x sin 23,42o) = 642 мм В соответствии с ГОСТ принимаем R = 660 мм. Задача 2.2.1.11. Из рис. 2.4. видно, что а = - а, где а = arctg ((Dа/D) x tg). Угол = + i = arcsin D/2R + i = arcsin(450/1200) + 25o = 47o Угол а = arctg (Dа/D tg) = arctg((344/450) x tg47o) = 39,34o Затылочный угол Deа = 35o - 39,34o = -4,34o.

Рисунок 2.5. Задача 2.2.1.12. При движении лапа встречает стебель. Сила сопротивления стебля R (рис. 2.5.) дает составляющую Т, которая стремится сдвинуть стебель по лезвию. Сдвижению стебля препятствует сила трения F. Скольжение стеблей по лезвию облегчает перерезание их и устраняет обволакивание лапы в случае, если перерезания не происходит. Условие скольжения стебля по лезвию Т > F, где Т = Rcos; F = Ntg = R sin tg. Учтя значения Т и F, получим Rcos > Rsin tg. Поделим обе части неравенства на Rsin: ctg > tg или tg(90o - ) > tg и 90o - > ; откуда < 90o - = 90o - arctg0,97 = 45,9o. Угол раствора лезвий стрельчатой лапы 2 <= 91,8o.

Рисунок 2.6. Задача 2.2.1.13. Лапа, перемещаясь в почве, погружается на глубину a (рис. 2.6.). Зона деформации почвы в продольном направлении ограничивается линией nm, расположенной под углом к нормали, проведенной через носок лапы. С боковых сторон зона деформации ограничивается плоскостями, расположенными к линии nm под углом /2. Из рисунка следует, что ширина разрыхленной полоски почвы равна b1 = b + 2 nm tg/2, где nm = a/cos( + ); угол трения = arctg 0,47 = 25,2o. С учетом этого Расстояние между лапами в ряду (культиватор трехрядный, рис.2.7.): Bл = 3( b1 - b) = 3 x (22,6 - 3) = 59 см. Расстояние между рядами лап: Z = L + L0 = a x tg( + ) + L0 = 12 x tg53,2o + 20 = 36 см.

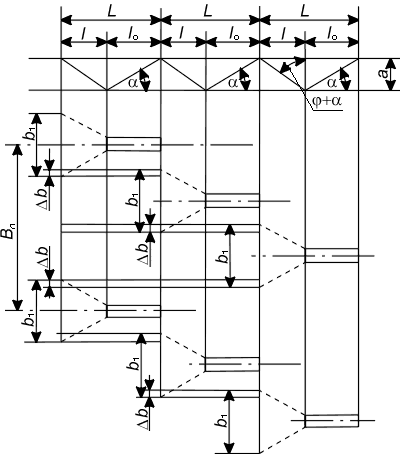Рисунок 2.7.

Задача 2.2.1.14. (см. Рис. 2.8.)
1. Подача на нож - это перемещение машины за время поворота барабана на угол 2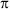/Z', где Z' - число ножей, работающих друг за другом, в нашем случае Z' = 3 (на рис. Ножи А, В и С).
За один оборот барабана машина проходит путь X_т = V_мТ = V_м x 60/n.
Подача на нож X_z = X_т/Z' = 1,1 x 60 / (240 x 3) = 0,092 м = 92 мм.
2. Абсолютное движение ножа складывается из относительного движения вокруг оси барабана с угловой скоростью 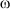и переносного перемещения со скоростью V_м. Для построения траектории абсолютного движения конца ножа от исходного положения вала I откладываем отрезок, равный X_т. Затем делим этот отрезок и окружность радиусом R на одинаковое число равных частей, например на 12 частей. Точки I, II, III и т.д. Определяют положение вала барабана в данный момент времени. Складывая поступательное перемещение и относительное движение конца ножа за данный отрезок времени, находим положение ножа в абсолютном движении ( точки А₂, А₃, А₄ и т. д.). На рис. 1.14. построены траектории абсолбтного движения крайних точек ножей А и В.
3. Толщину стружки определяем следующим образом. При глубине обработки почвы а ножи А и В входят в почву в точках А_вх и В_вх. Сечение снимаемой стружки определяется заштрихованной площадью между траекториями движения ножей. Толщину стружки измеряют по линии продолжения радиуса R = A_вхО_вх. Приближенно толщина стружки может быть равной отрезку А_вхЕ, то есть 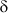= А_вхЕ = X_z cos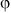_вх, где 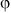_вх - угол входа ножа в почву. Из рисунка следует, что sin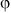_вх = (R - a)/R = 1 - a/R = 1 - m, где m = a/R = 10/17,5 = 0,57.
Тогда толщина стружки равна

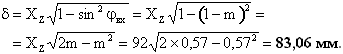
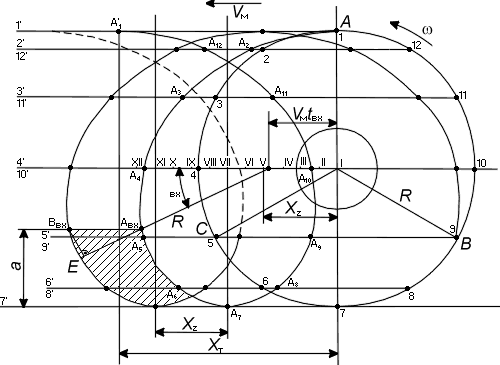Рисунок 2.8.

Рисунок 1.6. Задача 2.2.1.15. (см. Рис. 1.6.) По условию задачи в момент входа ножа в почву горизонтальная составляющая абсолютной скорости ножа Vx = 0. Составляющая Vx = dx/dt, где X = VMt + R cos t. Обозначим момент входа ножа в почву tвх = t1 и угол входа tвх = t1 = 1, тогда X1 = VM t1 + R cos t1 и VX1 = VM - R sin t1. Так как VX1 = 0, то sin t1 = sin 1 = VM/R =1/. С другой стороны sin 1 = (R-a)/a = 1 - m, где m = a/R = 10/17,5 = 0,57. Тогда показатель кинематического режима работы фрезы можно определить по формуле = 1/(1-m). При m = 0,57 показатель = 1 / (1-0,57) = 2,33. Угловая скорость вращения барабана = (VM)/R = (2,33 x 1,4) / 0,175 = 18,6 рад/с. Частота вращения барабана: n = 30/ = 18,6 x 30 / 3,14 = 178 мин-1.

Рисунок 2.9. Задача 2.2.1.16..( см. Рис. 2.9.) Теоретическая высота гребешков hrm = hr/K = 2/0,5 = 4 см. Найдем зависимость между hrm и показателем кинематического режима работы фрезы = R/VM. Абцисса вершины гребешка XB = Vмв/ + R cos в, абцисса точки А2: X2 = VМ /2 (здесь t2 = /2 и сost2 = 0). Так как VM = R/, то имеем: xв = (R/ x в) + Rcosв (1) и X2 = R/ x /2 (2). Из рисунка следует, что Xв = X2 + Xz/2, где Xz = 2R/Z - подача на нож. С чуетом этого координата Xв будет равна: Xв = R/ x /2 + 2R/2Z или Xв = R/ (0,5 + 1/Z) (3). Приравняв правые части выражений (1) и (3) и сделав упрощения, получим: (0,5+1/Z) = в + cosв (4) Высота гребешков hrm = yr = R - Rsinв, откуда Подставим значения в и cosв в уравнение (4) и найдем:

Задача 2.2.1.17. Мощность, необходимую для работы фрезы определяют по формуле: N = N_п + N_ф + N_тр - N_под,
где N_п - мощность на передвижение фрезы,
N_ф - мощность на фрезерование почвы,
N_тр - мощность на трение в передачах,
N_под - мощность на подталкивание барабана вперед.
1. Мощность на передвижение фрезы: N_п = f G V_м = 0,2 x 20000 x 0,875 = 3500 Вт = 3,5 кВт.
2. Мощность на фрезерование: N_ф = N_p + N_o;
Здесь N_p - мощность на резание,
N_o - мощность на отбрасывание почвы.
Мощность на резание N_p = 10³K_g X_z b_c a z n / 60,
где K_g - коэффициент сопротивления деформации почвы;
K_g = 0,15 МПа;
X_z - подача на один нож;
X_z = V_м 60 / nz' = 0,875 x 60 / 234 x 4 = 0,056 м;
b_c - ширина стружки, снимаемой ножом; b_c = 0,067 м;
a - глубина фрезерования; a = 0,20 м;
z - общее число ножей; z = 120;
n = 234 мин^-1;
N_p = 103 x 0,15 x 0,056 x 0,067 x 0,20 x 120 x 234 / 60 = 52,65 кВт.
Мощность на отбрасывание почвы: N_o = 0,5 K_o B a V_м V_p² ,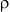
где K_o - коэффициент отбрасывания; для болотных ножей K_o = 1,0;
B - ширина захвата фрезы; B = 2 м.
V_p = V_ok - V_м = (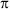 D n / 60) - V_м = (3,14 x 0,71 x 234 / 60) - 0,875 = 8,69 - 0,875 = 7,815 м/с.
N_o = 0,5 x 1,0 x 2 x 0,2 x 0,875 x 7,8152 x 1300 = 13894 Вт = 13,9 кВт.
Мощность на фрезерование: N_ф = 52,65 + 13,9 = 66,55 кВт.
3. Мощность на трение в передачах: N_тр = N_ф x (1- 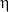_п) = 66,55 x (1 - 0,98) = 1,33 кВт.
4. Мощность на подталкивание фрезерного барабана: N_под = N_под x V_м / V_ok = 66,55 x 0,875 / 8,69 = 6,7 кВт.
5. Полная мощность: N_пол = 66,55 + 3,5 + 1,33 - 6,7 = 64,68 кВт.

astets@karelia.ru
Создано 05 Мая 1998
Отредактировано 15 Июня 1998