Получить опытным путем линейные размеры (длину, ширину, толщину) компонентов зерновой смеси; определить расчетом или с использованием ПЭВМ вероятностные характеристики распределения компонентов смеси; выбрать форму и размер отверстий решет или ячеек триера для разделения исследуемой смеси.
Для выполнения работы требуется линейный классификатор или штангенциркуль, решетный классификатор с набором решет.
Различие в линейных размерах семян основной культуры и засорителей используется при выборе средств очистки и сортировки. Путем анализа, например, длины всех компонентов зерновой смеси можно определить их числовые и построить графические характеристики, выбрать триеры для разделения.
При выполнении расчетов предполагают, что линейные размеры смеси являются случайными величинами с нормальным законом распределения:
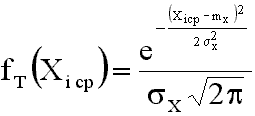
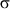 x - соответственно среднее значение размера и его среднеквадратическое отклонение;
x - соответственно среднее значение размера и его среднеквадратическое отклонение;
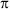 = 3,14.
= 3,14.
При этом считают, что изменения любого размера находятся в диапазоне 6 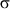 x, т.е. Xmax = mx + 3
x, т.е. Xmax = mx + 3 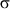 x и Xmin = mx -
x и Xmin = mx - 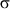 x.
x.
Числовые характеристики определяются выражениями:
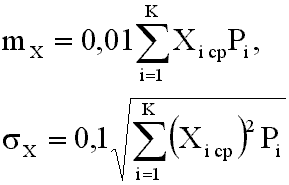
Графические характеристики случайных величин выражаются:
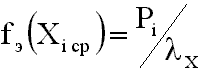
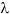 x = (Xmax - Xmin) / K - классовый интервал;
x = (Xmax - Xmin) / K - классовый интервал;
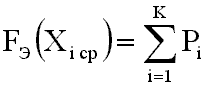
Принимая во внимание, что линейные размеры смеси подчиняются нормальному закону распределения, теоретическую плотность распределения можно получить и с использованием табулированной функции, при этом
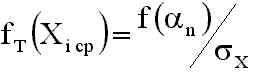
Из навески зерновой смеси выделяют три компонента: длинные примеси, зерно и короткие примеси. Линейным классификатором замеряется, например, длина всех компонентов смеси (количество измерений указывается преподавателем).
Результаты измерений заносятся в таблицу 1.
| N п/п | Длина, мм | ||
|---|---|---|---|
| длинные примеси | зерно | короткие примеси | |
| 1. 2. 3. ... | |||
На основании данных табл.1 для каждого компонента смеси определяют значения Xmin и Xmax, число классов К, классовый интервал 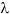 x, границы классов.
x, границы классов.
Чтобы избежать одностороннего смещения границ классов, определяют их смещение в сторону меньших и больших значений величины признака. При этом
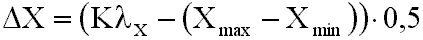
При определении границ классов нижнюю границу первого класса смещают от X в сторону меньших значений аргумента, а верхнюю границу последнего класса - от Xmax в сторону больших значений аргумента.
Нижняя граница первого класса равна X1Н = Xmin - 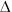 X, а верхняя граница первого класса X1В = X1Н +
X, а верхняя граница первого класса X1В = X1Н + 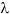 x.
x.
Соответственно границы второго класса определяются, как X2Н = X1В = X1Н + 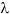 x и X2В = X1Н + 2
x и X2В = X1Н + 2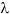 x и т.д.
x и т.д.
Верхняя граница класса равна XКВ = Xmax + 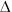 X.
X.
Середина классов определяется в виде Xi cp = 0.5 (XiН + XiВ ).
Подсчитывают число зерен n в каждом классе (частоту классов), вычисляют относительное количество Pi семян в классе (относительная частота классов) и получают эмпирическую плотность распределения fэ(Xi cp).
Для вычисления эмпирической функции распределения (накопленной частоты) используют выражение
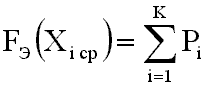
На основании полученных результатов заполняют таблицу 2.
| Классы | 1 | 2 | ... | ||||
|---|---|---|---|---|---|---|---|
| X1Н | X1В | X2Н | X2В | ... | ... | ||
| Границы классов
Хi, мм | длинные примеси зерно короткие примеси | ||||||
| Середины классов
Хi cp, мм | длинные примеси зерно короткие примеси | ||||||
| Частота классов
ni, шт | длинные примеси зерно короткие примеси | ||||||
| Частость классов
Рi =(ni/N), 100% | длинные примеси зерно короткие примеси | ||||||
| Плотность распределения
fэ(Xi cp) | длинные примеси зерно короткие примеси | ||||||
| Функция распределения
Fэ(Xi cp) | длинные примеси зерно короткие примеси | ||||||
| (Xi cp) Pi | длинные примеси зерно короткие примеси | ||||||
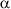 i = (Xi cp) - mx i = (Xi cp) - mx
| длинные примеси зерно короткие примеси | ||||||
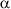 i2 i2
| длинные примеси зерно короткие примеси | ||||||
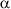 i2 Pi i2 Pi
| длинные примеси зерно короткие примеси | ||||||
| Среднее значение
mx, мм длинные примеси | зерно короткие примеси | ||||||
| Среднеквадратическое отклонение +/- 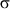 ,мм ,мм
| длинные примеси зерно короткие примеси | ||||||
По форме табл. 2 аналогично выполняют расчет вероятностных характеристик распределения для зерна и коротких примесей.
На основании результатов вычислений (табл. 2) строят графики для зерна, длинных и коротких примесей. По кривым Fэ(Xi cp) выбирают рабочую величину, например, диаметр ячеек триеров.
Расчет числовых и построение графических характеристик зерновой смеси может быть выполнен на ПЭВМ с использованием программы "SEM". Программа написана на языке Турбо-Бейсик в диалоговом режиме с пользователем.
В соответствии с запросом можно получить распечатку таблиц для построения гистограммы, полигона и интегральной кривой, теоретической плотности распределения, критерия Пирсона, а также графики гистограммы, полигона, интегральной кривой и теоретической плотности распределения.
Отчет должен содержать:


